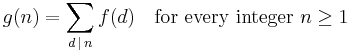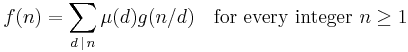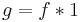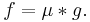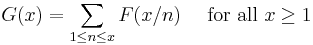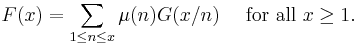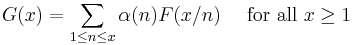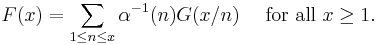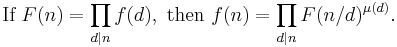Möbius inversion formula

In mathematics, the classic Möbius inversion formula was introduced into number theory during the 19th century by August Ferdinand Möbius.

Other Möbius inversion formulas are obtained when different local finite partially ordered sets replace the classic case of the natural numbers ordered by divisibility; for an account of those, see incidence algebra.

Contents

Statement of the formula

The classic version states that if g(n) and f(n) are arithmetic functions satisfying

g(n)=\sum_{d\,\mid \,n}f(d)\quad\text{for every integer }n\ge 1

then

f(n)=\sum_{d\,\mid\, n}\mu(d)g(n/d)\quad\text{for every integer }n\ge 1

where μ is the Möbius function and the sums extend over all positive divisors d of n. In effect, the original f(n) can be determined given g(n) by using the inversion formula. The two sequences are said to be Möbius transforms of each other.

The formula is also correct if f and g are functions from the positive integers into some abelian group (viewed as a Z-module).

In the language of Dirichlet convolutions , the first formula may be written as

g=f*1

where * denotes the Dirichlet convolution, and 1 is the constant function 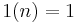1(n)=1. The second formula is then written as

f=\mu * g.

Many specific examples are given in the article on multiplicative functions.

Repeated transformations

Given an arithmetic function, one can generate a bi-infinite sequence of other arithmetic functions by repeatedly applying the first summation.

For example, if one starts with Euler's totient function \varphi, and repeatedly applies the transformation process, one obtains:

  1. \varphi the totient function
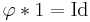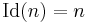  2. \varphi*1=\operatorname{Id} where \operatorname{Id}(n)=n is the identity function
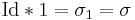  3. \operatorname{Id} *1 =\sigma_1 =\sigma, the divisor function

If the starting function is the Möbius function itself, the list of functions is:

  1. \mu, the Möbius function
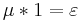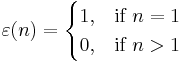  2. \mu*1 = \varepsilon where \varepsilon(n) = \begin{cases} 1, & \mbox{if }n=1 \\ 0, & \mbox{if }n>1 \end{cases} is the unit function
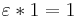  3. \varepsilon*1 = 1 , the constant function
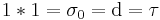  4. 1*1=\sigma_0=\operatorname{d}=\tau, where 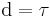\operatorname{d}=\tau is the number of divisors of n, (see divisor function).

Both of these lists of functions extend infinitely in both directions. The Möbius inversion formula enables these lists to be traversed backwards. The generated sequences can perhaps be more easily understood by considering the corresponding Dirichlet series: each repeated application of the transform corresponds to multiplication by the Riemann zeta function.

Generalizations

See also: Incidence algebra

An equivalent formulation of the inversion formula more useful in combinatorics is as follows: suppose F(x) and G(x) are complex-valued functions defined on the interval [1,∞) such that

G(x) = \sum_{1 \le n \le x}F(x/n)\quad\mbox{ for all }x\ge 1

then

F(x) = \sum_{1 \le n \le x}\mu(n)G(x/n)\quad\mbox{ for all }x\ge 1.

Here the sums extend over all positive integers n which are less than or equal to x.

This in turn is a special case of a more general form. If 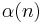\alpha(n) is an arithmetic function possessing a Dirichlet inverse 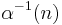\alpha^{-1}(n), then if one defines

G(x) = \sum_{1 \le n \le x}\alpha (n) F(x/n)\quad\mbox{ for all }x\ge 1

then

F(x) = \sum_{1 \le n \le x}\alpha^{-1}(n)G(x/n)\quad\mbox{ for all }x\ge 1.

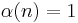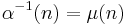The previous formula arises in the special case of the constant function \alpha(n)=1, whose Dirichlet inverse is \alpha^{-1}(n)=\mu(n).

Multiplicative notation

As Möbius inversion applies to any abelian group, it makes no difference whether the group operation is written as addition or as multiplication. This gives rise to the following notational variant of the inversion formula:

\mbox{If } F(n) = \prod_{d|n} f(d),\mbox{ then } f(n) = \prod_{d|n} F(n/d)^{\mu(d)}. \,

See also

References